Is fit robust to descending data?
Posted: Wed Sep 28, 2022 3:16 am
Hi all-
I'm trying to fit a psychometric curveto aggregate subject data using PAL_PFHB_fitModel, but the fit doesn't look right.
Here are some code snippets:
data.x = [24, 16, 8, 4, 2, 1, 0.5, 0]; % Stimulus rotation
data.y = [134, 140, 208, 324, 338, 334, 326, 346];
data.n = [384, 384, 384, 384, 384, 384, 384, 384];
For simplicity, when I run:
pfhb = PAL_PFHB_fitModel(data, 'PF': 'weibull')
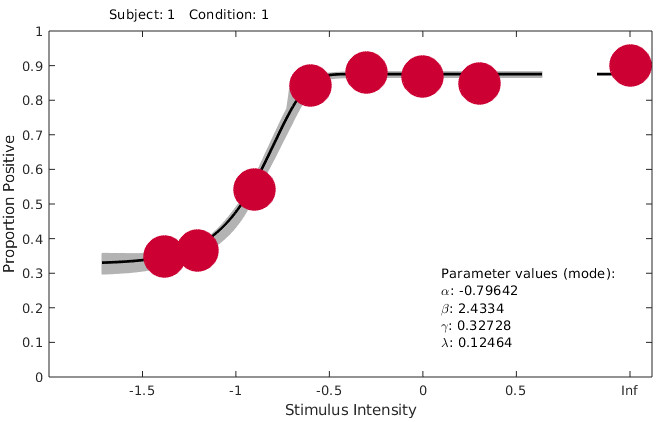
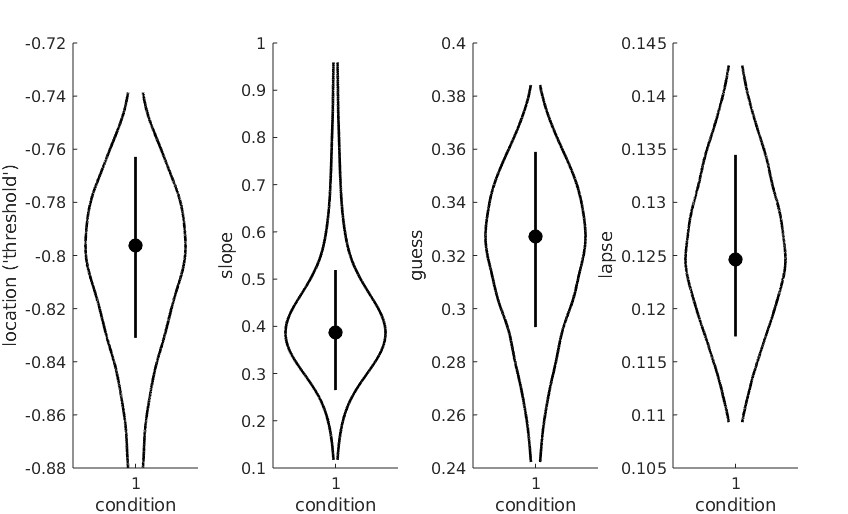
I get this fit: I've tried different fits and I've also reversed the stimulus intensity values from 24, 16.. to 0, 0.5.. without changing the position of the data.y values, which of course is wrong, but leads me to the suspicion that Palamedes requires smaller intensity values to be associated with smaller response rates (i.e., an ascending psychometric curve as opposed to descending, which would be my data). Is that a correct assumption or am I missing something?
If that is indeed the case, does anyone know how I could solve this issue?
I'm trying to fit a psychometric curveto aggregate subject data using PAL_PFHB_fitModel, but the fit doesn't look right.
Here are some code snippets:
data.x = [24, 16, 8, 4, 2, 1, 0.5, 0]; % Stimulus rotation
data.y = [134, 140, 208, 324, 338, 334, 326, 346];
data.n = [384, 384, 384, 384, 384, 384, 384, 384];
For simplicity, when I run:
pfhb = PAL_PFHB_fitModel(data, 'PF': 'weibull')
I get this fit: I've tried different fits and I've also reversed the stimulus intensity values from 24, 16.. to 0, 0.5.. without changing the position of the data.y values, which of course is wrong, but leads me to the suspicion that Palamedes requires smaller intensity values to be associated with smaller response rates (i.e., an ascending psychometric curve as opposed to descending, which would be my data). Is that a correct assumption or am I missing something?
If that is indeed the case, does anyone know how I could solve this issue?